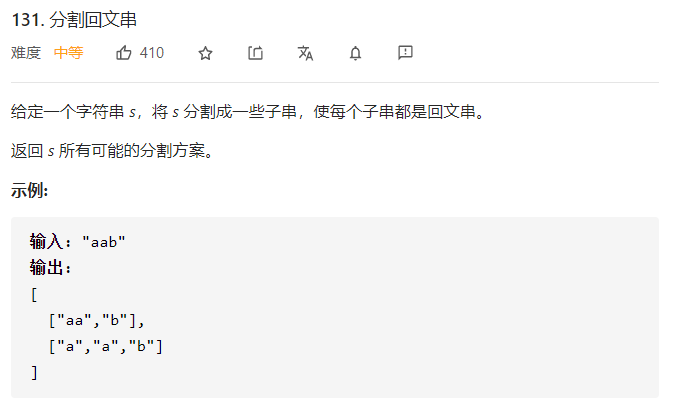
题目分析
这个题目和Leetcode 140题非常类似,在140题中是判断分割字符是否出现在字典中,这个题目是判断分割字符是否为回文,两个题目的解法是几乎相同的,小伙伴们可以做一题,用另一题练习。
动态规划
这种题目可以先尝试使用动态规划进行求解。dp[i]代表前i个字符组成的结果。因此计算dp[i]时,j要遍历从0到i - 1的所有情况,如果从j到i的单词为回文字符串中,那么dp[i]可以由dp[j]中的所有结果后面添加该单词组成。
如”abb”字符串,当i=3时,求解dp[i],j从0遍历到i - 1,j=1时,dp[1]=[[“a”]]是已知的,而且从第二个字符到第三个字符为”bb”是回文字符串,因此dp[3]可以由dp[1]在后面添加”bb”组成,此时dp[3]=[[“a”, “bb”]]。j=2时,dp[2]=[“ab”]是已知的,而且从第三个字符到第三个字符为”b”是回文字符串,因此dp[3]可以由dp[2]在后面添加”b”组成,此时dp[3]=[[“a”, “bb”], [“ab”, “b”]]。
算法的**时间复杂度为$O(n^n)$,空间复杂度为$O(n^n)$**。
1 | from functools import lru_cache |
DFS
DFS的思想和DP基本相同,也是判断前面的字符是否为回文字符串,如果是则加入字符串中,并且继续寻找接下来的字符是否为回文字符串,代码非常简单,因为dp[i]需要用到dp[j]的数据,因此动态规划需要进行数据拷贝,而DFS不需要数据拷贝,只需要进入下一层栈空间即可,因此代码量相对较少,思路也比较清晰。
上面是求回文串的记忆化搜索方法,在这里给出了一种求回文串的DP方法。
算法的**时间复杂度为$O(n^n)$,空间复杂度为$O(2^n)$**。
1 | class Solution: |
优化DFS
虽然DFS更加简单,但是本质上并没有降低算法的时间复杂度,仍然存在着大量的冗余计算过程。
那么如何进行优化呢?我们发现DFS算法在一个极端的例子。字符串为”aaaaaa”,cur=[“a a a”],s=”aaa”和cur=[“a”, “aa”],s=”aaa”的时候,都需要迭代计算s。其实无论是哪种情况,迭代s返回的结果都一样,因此不需要重复计算。
这时我们就要利用记忆化的思路,保存计算的中间结果。传递的参数为字符串的位置,当传入相同的位置时,只需要计算一次即可。
算法的**时间复杂度为$O(2^n)$,空间复杂度为$O(2^n)$**。
1 | from functools import lru_cache |
刷题总结
记忆化是非常重要的考察内容之一,在DFS中十分常见,普通的DFS难度较小,因此增加记忆化提高难度,也符合现在笔试面试的要求。